Trijstūra perimetrs: jēdziens, raksturīgums, noteikšanas veidi

Trijstūris ir viens no fundamentālajiem aspektiemģeometriski skaitļi, kas attēlo trīs taisnās līnijas, kas krustojas. Šis skaitlis bija zināms Senās Ēģiptes, Senās Grieķijas un senās Ķīnas zinātniekiem, kuri līdz mūsdienām atrada lielāko daļu formulu un likumu, ko izmanto zinātnieki, inženieri un dizaineri.

Galvenie trīsstūra sastāvdaļas ir:

• Virzieni ir segmentu krustošanās punkti.

• Sānos ir krustošanās līniju segmenti.

Pamatojoties uz šiem komponentiem, formulējiettādi jēdzieni kā trijstūra perimetrs, tā apgabals, ierakstīts un ierobežots aplis. Kopš skolas ir zināms, ka trijstūra perimetrs ir visu triju pušu summas skaitliskā izteiksme. Tajā pašā laikā zināms daudzums formulu ir zināms, lai noteiktu noteiktu vērtību, atkarībā no tiem sākotnējiem datiem, kas pētniekam ir vienā vai citā gadījumā.

1. Vienkāršākais veids, kā atrast trijstūra perimetru, tiek izmantots gadījumā, ja visu to trīs sānu (x, y, z) skaitliskās vērtības ir zināmas kā sekas:

P = x + y + z

2 Vienādmalu trīsstūra perimetru var atrast, ja atceramies, ka šajā attēlā visas puses, tāpat kā visi leņķi, ir vienādi. Zinot šīs puses garumu, vienādmalu trīsstūra perimetru var noteikt pēc formulas:

P = 3x

3 Vienādmalu trīsstūrī, atšķirībā no vienādmalu trīsstūra, tikai divas sānu malas ir vienādas skaitliskās vērtības, tādēļ šajā gadījumā kopumā perimetrs būs šāds:

P = 2x + y

4 Gadījumos, kad ir zināmas ne visas puses skaitliskās vērtības, ir nepieciešamas šādas metodes. Piemēram, ja pētījumā ir dati no divām pusēm un leņķis starp tiem ir zināms, tad trīsstūra perimetru var atrast, nosakot trešo pusi un zināmo leņķi. Šajā gadījumā šī trešā persona tiks atrasta pēc formulas:

z = 2x + 2y-2xycosβ

Pamatojoties uz šo, trijstūra perimetrs būs:

P = x + y + 2x + (2y-2xycos β)

5 Gadījumā, ja sākotnēji tiek norādīts garums ne vairāk kā vienā trijstūra malā, un ir zināmi divu leņķu skaitliskie lielumi blakus tam, trijstūra perimetru var aprēķināt, pamatojoties uz sinusu teorēmu:

P = x + sinβ x / (sin (180 ° -β)) + sinγ x / (sin (180 ° -γ))

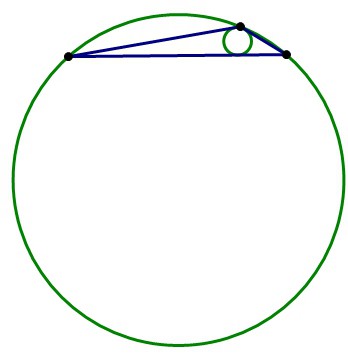
6. Ir gadījumi, kad apzīmēto loku zināmie parametri tiek izmantoti, lai atrastu trijstūra perimetru. Šī formula ir zināms arī lielākajai daļai cilvēku kopš skolas dienas:

P = 2S / r (S ir apļa laukums, bet r ir tā rādiuss).

No visa iepriekš minētā var redzēt daudzumuTrijstūra perimetru var atrast dažādos veidos, balstoties uz pētnieka datiem. Turklāt ir daži īpaši konkrēti konkrētas vērtības noteikšanas gadījumi. Tādējādi perimetrs ir viens no svarīgākajiem taisnleņķa trīsstūra daudzumiem un īpašībām.

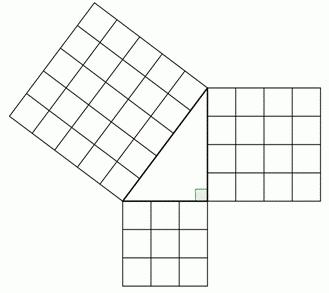
Kā zināms, šāds trijstūris tiek sauktsforma, abas puses, kuras veido pareizo leņķi. No trijstūris perimetrs ir summa no ciparu izteiksmes caur abām kājām un hipotenūza. Šajā gadījumā, ja pētnieks zināms datus tikai no divām pusēm, atlikums var aprēķināt, izmantojot labi zināmo Pitagora teorēmu: z = (x2 + y2), ja tas ir zināms, gan kāju, vai x = (z2 - y2), ja tas ir zināms hipotenūzas un kāju.

Gadījumā, ja hipotenūza garums ir zināms unviens no leņķiem, kas tam blakus atrodas, tad pārējās abas puses norāda pēc formulas: x = z sinβ, y = z cosβ. Šajā gadījumā taisnleņķa trīsstūra perimetrs būs:

P = z (cosβ + sinβ + 1)

Arī īpašs gadījums ir aprēķinsperimetrs no regulārā (vai vienādmalu) trīsstūra, tas ir, skaitlis, kurā visas puses un visi leņķi ir vienādi. Šāda trijstūra perimetra aprēķināšana zināmai pusei nav problemātiska, tomēr pētnieks bieži zina dažus citus datus. Tātad, ja ir zināms apzīmējuma apļa rādiuss, regulārā trīsstūra perimetrs tiek atrasts pēc formulas:

P = 6√3r

Un, ja tiek norādīts ierobežotā apļa rādiuss, regulārā trīsstūra perimetrs tiks atrasts šādi:

P = 3, 3R

Formulas ir jāiegaumē, lai tās varētu veiksmīgi pielietot praksē.